[Programmers] 2 x n 타일링
문제 설명
문제 설명
가로 길이가 2이고 세로의 길이가 1인 직사각형모양의 타일이 있습니다. 이 직사각형 타일을 이용하여 세로의 길이가 2이고 가로의 길이가 n인 바닥을 가득 채우려고 합니다. 타일을 채울 때는 다음과 같이 2가지 방법이 있습니다.
- 타일을 가로로 배치 하는 경우
- 타일을 세로로 배치 하는 경우
예를들어서 n이 7인 직사각형은 다음과 같이 채울 수 있습니다.

직사각형의 가로의 길이 n이 매개변수로 주어질 때, 이 직사각형을 채우는 방법의 수를 return 하는 solution 함수를 완성해주세요.
제한사항
- 가로의 길이 n은 60,000이하의 자연수 입니다.
- 경우의 수가 많아 질 수 있으므로, 경우의 수를 1,000,000,007으로 나눈 나머지를 return해주세요.
입출력 예
| n | result |
|---|---|
| 4 | 5 |
입출력 예 설명
입출력 예 #1 다음과 같이 5가지 방법이 있다.





문제 풀이
# 동적계획법
풀이 과정
아는 사람은 정말 쉽게 풀고, 모르는 사람은 해메는 동적계획법의 대표적인 문제입니다.
문제를 처음 보고는 ‘아, 눕혀서 배치한 2*2 블록의 개수로 풀면 되겠다’라고 생각했지만, 문제의 입력이 너무 크기 때문에 조합을 계산하면 메모리 초과/시간 초과가 필연적으로 발생합니다.
이 문제는, 구조의 유사성을 발견해야 합니다.
DP문제를 접근하기 위해서 케이스를 나눠봅시다.
케이스를 나눌 때는 문제를 다 풀기 직전의 상황부터 거꾸로 푸는 방법이 좋습니다. (TOP-DOWN 접근)
문제에서 바닥의 세로 길이는 2로 고정되어있고, 가로의 길이는
60,000이하의 자연수 입니다. 따라서, 가로의 길이를 기준으로 케이스를 나누는 방향으로 진행하여야 합니다.위의 문제에서의 경우의 수는 총 2가지입니다.
첫번째 케이스(N-1)는 다음과 같습니다.
채울 수 있는 가로의 길이는 1밖에 없으므로 1가지 경우만 나옵니다.
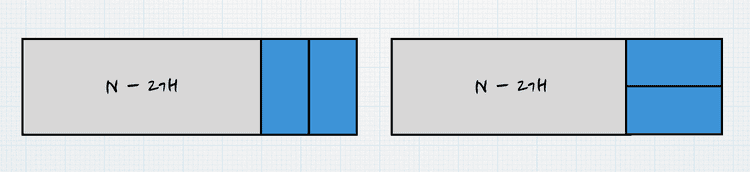
두번째 케이스(N-2)는 다음과 같습니다.
하지만 여기서 왼쪽 케이스는 위의 첫번째 케이스에 포함되는 모양입니다.
따라서, 왼쪽 케이스는 개수에 포함하지 않습니다.
그렇다면 세번째 케이스는?
N-3개인 경우의 모양을 만들면 위의 N-1, N-2의 케이스에 모두 포함되는 모양이 나와 개수에 포함하지 않습니다.결과적으로 위의 상황을 점화식으로 만들면?!
DP(n) = DP(n-1) + DP(n-2)
참조: https://wwlee94.github.io/category/algorithm/dp/2xn-tiling/
따라서 이는 동적 계획법 문제이며, 피보나치 수열(dp[i] = dp[i-1] + dp[i-2])과 같은 형태의 점화식을 가집니다.
전체 코드
1번 풀이: 런타임 에러/시간 초과
조합의 개수를 더해 풀려고 하였지만 입력의 크기가 커서 통과할 수 없습니다.
def solution(n):
# 눕힌(1*2) 꼴로 배치해서 2*2를 만드는 개수를 고려
# n: 짝수(2m)/n: 홀수(2m+1) -> 0, 1, ..., m 개 -> (n-m)Cm
def nCk(n, k):
numerator, denominator = 1, 1
k = min(n-k, k) # 조합의 대칭성을 이용
for i in range(1, k+1):
denominator *= i % (1e+9 + 7)
numerator *= n+1-i % (1e+9 + 7)
return numerator/denominator % (1e+9 + 7)
ans = 0
for m in range(n//2+1):
ans += nCk(n-m,m) % (1e+9 + 7)
return ans
2번 풀이: 정답
동적 계획법을 이용하여 bottom-top 방식으로 규칙성을 찾아 풀이합니다.
def solution(n):
# 구조의 유사성/반복성을 이용하여 dp로 풀이 -> 피보나치 수열
dp = [0 for _ in range(n+1)]
dp[1], dp[2] = 1, 2
for i in range(3,n+1):
dp[i] = (dp[i-1] + dp[i-2]) % (1e9 + 7)
return dp[n]
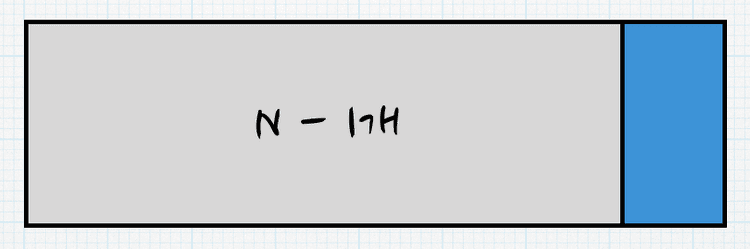
Leave a comment