[AITech] 20220209 - Attention&Transformer

학습 내용

이번 포스팅에서는 강력한 성능을 보여주는 Transformer를 중심으로 Encoder, Decoder, 그리고 그 내부에 있는 Attention의 구조와 동작 방식에 대해 알아보려 합니다.

(이번 포스팅에서 사용하는 자료의 대부분은 여기에서 가져왔습니다)

What is Transformer?

간단하게 Transformer가 무엇인지에 대한 얘기부터 해봅시다.

Transformer는 본래 자연어 번역을 위한 모델로, RNN 구조 없이 Attention이라는 모듈을 도입해서 매우 성공적인 performance를 보인 모델입니다.

Transformer의 구조는 아래와 같습니다.

구조를 보면 아래와 같은 정보들을 발견할 수 있습니다.

• Transformer는 기계 번역 task를 수행합니다.
• Transformer는 Encoder 부와 Decoder 부로 나눠져 있습니다.
• Encoder와 Decoder 부는 각각 6개의 stacked 구조로 되어 있습니다.

그럼 이제 Transformer가 무엇을 하는 녀석이고, 어떤 구조로 되어 있는지 봤으니, 각각의 부분들을 하나씩 뜯어봅시다.

Encoder

Encoder의 구조 내부는 아래와 같이 생겼습니다.

그러면 이제 저 Self-Attention 모듈이 무엇이고, 어떻게 RNN을 대체했는지에 대해 봐야겠죠?

Attention

Attention이 무엇인가?

우선 rough하게 말하면, Attention은 N개의 단어로 이루어진 문장을 처리할 때 재귀적으로 N번 처리하는 것이 아니라, 한 번에 N개의 단어를 모두 이용합니다. 다시 말하면, 1개의 단어를 처리하기 위해 다른 N-1개의 단어에 대한 정보를 동시에 활용하는 것입니다.

이렇게 함으로써 얻을 수 있는 이점은 무엇을까요? 첫째, 학습 시간을 줄일 수 있습니다. N번의 과정을 기다려야 했던 RNN에 비해, 이를 한 번에 처리하는 Transformer는 훨씬 빠른 모습을 보입니다. 둘째, 다른 단어들에 대한 정보를 더 잘 얻을 수 있습니다. RNN 모델에서는 긴 시계열 데이터에 대해 long term memory에 대한 한계가 있었다면, Attention 구조에서는 동시에 다른 단어들에 대한 정보를 이용하기 때문에 그런 문제가 없습니다.

다만, 당연하게도 많은 정보를 한 번에 이용하는 Attention 구조는 많은 Computational resource를 요구하긴 합니다. 이것이 Transformer의 한계로 지적되기도 하죠.

Attention의 동작 구조

어찌되었든, Attention은 N개의 단어를 함께 고려하며 각 단어에 대해 처리를 합니다. 아래처럼 말이죠.

위 그림을 보면 각 단어에 해당하는 x벡터가 Attention의 입력으로 들어가, 출력으로 z벡터들이 나오는데, 그 과정을 한 번 살펴봅시다.

Attention은 아래의 과정을 수행합니다.

1. x의 Input feature를 embedding하여 Embedded vector로 변환

2. 각각의 embedded vector에 대해 Query/Key/Value vector 한 쌍을 생성

3. 각 단어에 대해 자신을 포함한 모든 단어들과 Query vector와 Key vector를 내적
   • 이 값을 Attention Score라고 함
   • 이 Attention Score가 해당 단어와 다른 단어들과의 관계성을 나타내는 지표라고 할 수 있음
4. 각각의 score를 root(d_k)로 나누고 Softmax를 적용
   • 이 때의 d_k는 dimension of key vector
   • 이 값을 Attention weight라고 함
5. 나눈 값에 각각에 해당하는 단어의 Value vector를 스칼라 곱하고 모두 더함 (Weighted Sum)
   • 이 값을 z라고 함

아래는 2개의 단어로 이루어진 문장(Thinking Machines)에서 ‘Thinking’이라는 단어로부터 z 값을 도출하는 과정을 그림으로 표현한 것입니다.

위와 같은 과정으로 각각의 x에 대해 z를 구하는데요, 이로 인해 RNN에서 N번의 과정을 거쳐야 했던 변환은 Attention에서는 단순한 행렬곱으로 대체될 수 있습니다.

바로 아래와 같이, 단어들의 sequence를 행렬로 나타내면 각각 W^Q, W^K, W^V 행렬과 곱해서 바로 Q, K, V 행렬을 구할 수 있습니다.

그리고 위에서 구한 Q, K, V vector를 이용하면 아래와 같은 간단한 수식으로 x에서 z를 구할 수 있습니다.

이런 과정을 통해, Attention은 자연스럽게 다른 단어들과의 관계성을 학습하게 되죠.

MHA (Multi-Headed Attention)

그런데 실제로는, Transformer는 각 Encoder(또는 Decoder)마다 8개의 Attention을 병렬적으로 함께 사용합니다. 따라서 다음과 같이 8개의 z 벡터가 하나의 Encoder 내에서 생성됩니다.

이렇게 하는 이유는, 바로 아래와 같이 여러 관점에서 다른 단어들과의 관계를 구하기 위함입니다. 하나의 Attention만을 사용한다면, 그 Attention이 학습한 정보밖에는 활용하지 못 하는데 비해, 여러 개 Attention을 사용하면 여러 개의 관점으로 학습한 정보들을 모두 사용할 수 있다는 것이죠.

출력 형태 맞춰주기

위와 같은 과정으로 MHA를 통과하고 나면, 8개의 Z 행렬이 생성됩니다. 이제는 이 Z 행렬을 처음 입력 행렬이었던 X와 같은 형태로 맞춰줘야 합니다. 왜냐하면 Encoder 부에는 여러 개의 stacked encoder들이 있기 때문에 이번 encoder의 출력은 다음 encoder로의 입력이 됩니다.

이 과정은 단순히 행렬 Wo와 행렬곱함으로써 수행할 수 있습니다.

그래서 Self-Attention 모듈을 통과하는 과정은 아래와 같습니다. (Encoder에서는 Self-Attention 모듈 이후에 FC-layer를 지나야 함을 잊지 마세요!)

Positional encoding & Residual connection

여기까지의 과정이 이해되셨나요? 여기에 2가지만 더 추가해봅시다. 하나는 Positional encodding이고 다른 하나는 Residual connection입니다.

Positional Encodding

Sequential data를 다루는 모든 모델에서는 data들의 순서가 매우 중요합니다. 그런데 위의 과정만으로는, 그 단어들의 순서를 제대로 고려해주지 못합니다. 문장을 이루는 단어들이 같아도, 순서가 다르다면 다른 출력이 나올 수 있어야 하는데, 그러지 못하는 것이죠.

바로 이 단어들의 순서를 고려해주기 위한 것이 positional encodding입니다. 그리고 이는 단순히 Embedded vector에 Positional encodding을 위한 행렬을 더해줌으로써 수행할 수 있습니다.

논문에서는 이 positional encodding에 해당하는 값들을 sin, cos 값을 이용하여 생성하고, 이를 사용하는 이유는 그 값이 -1~1까지의 범위를 가지며 단어의 개수와 상관없이 몇 개든 만들어낼 수 있는 연속함수이기 때문이라고 합니다.

Residual Connection

두번째로, Residual connection입니다. Transformer의 학습 과정에서 backpropagation이 수행되다 보면, 위에서 본 positional encodding에 대한 정보가 손실되기 쉽습니다. 바로 이 정보를 견고히 유지하기 위해서 아래와 같이 Residual connection이 존재합니다.

(진짜 진짜 마지막으로, residual connection 다음에는 layer normalization이라는 것을 적용해서 학습 효과를 증진시킵니다 😊)

최종 인코더의 입출력 형태는 아래와 같습니다.

Encoder -> Decoder

다음으로 여기서는 Encoder 부를 모두 통과한 정보들이 Decoder 부에 어떻게 전달되는 지에 대해 알아보겠습니다. 여기까지 따라오셨다면 거의 다 왔습니다!!!

만약 우리가 2개의 인코더-디코더를 사용한다면 최종 Encoder 부의 출력은 아래 그림과 같이 Decoder 부에 전달되는데요, 과연 어떤 정보들이 전달되는 것일까요?

Encoder에서 K, V를 Decoder에 전달한다

Encoder 부에서 입력 x가 일련의 encoder들을 모두 지나고 나면, 위에서 본 것처럼 input x와 형상이 같은 output z가 출력될 것입니다. 이 최종 출력 z를 이용해 K와 V matrices를 생성하고, 이 두 행렬을 각각의 Decoder에게 전달합니다.

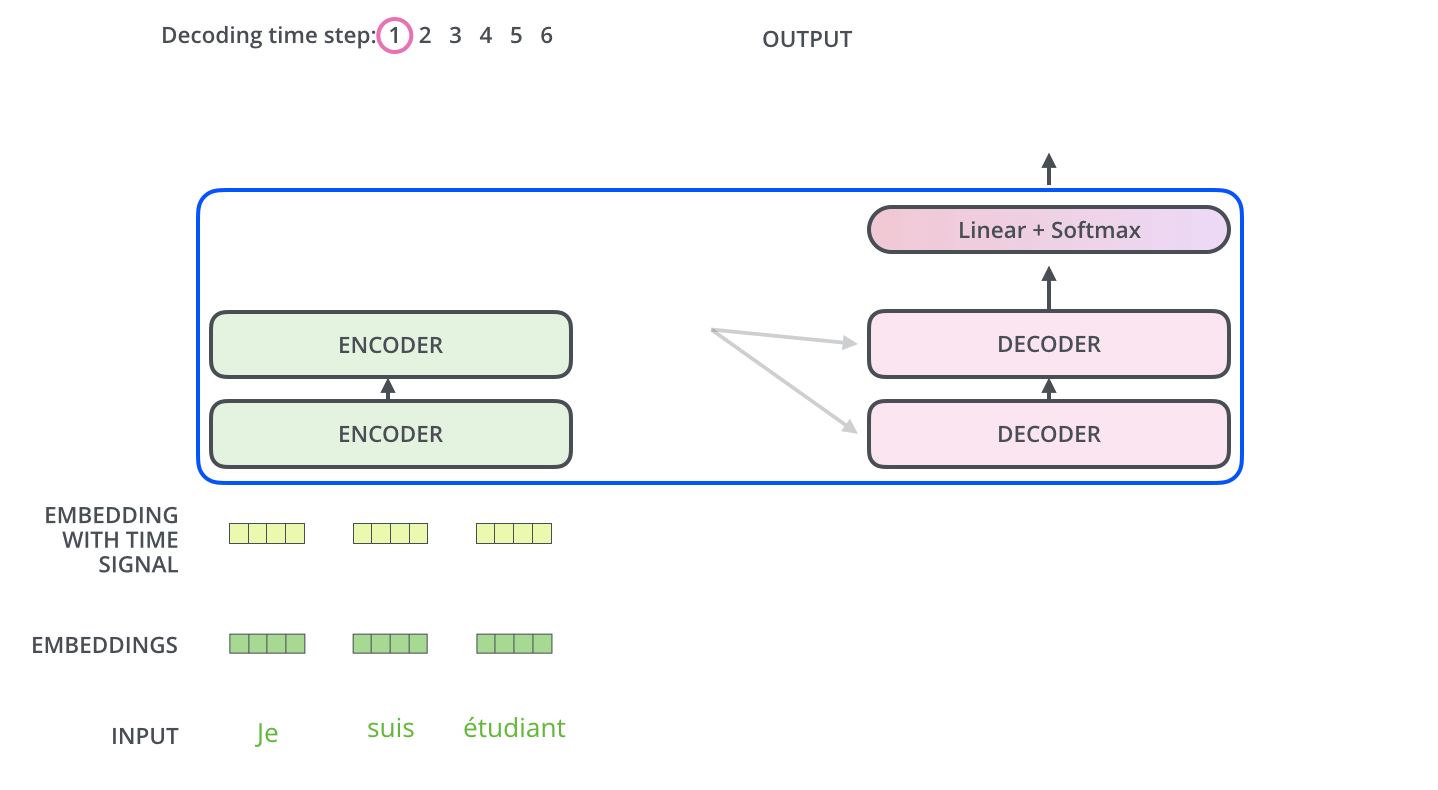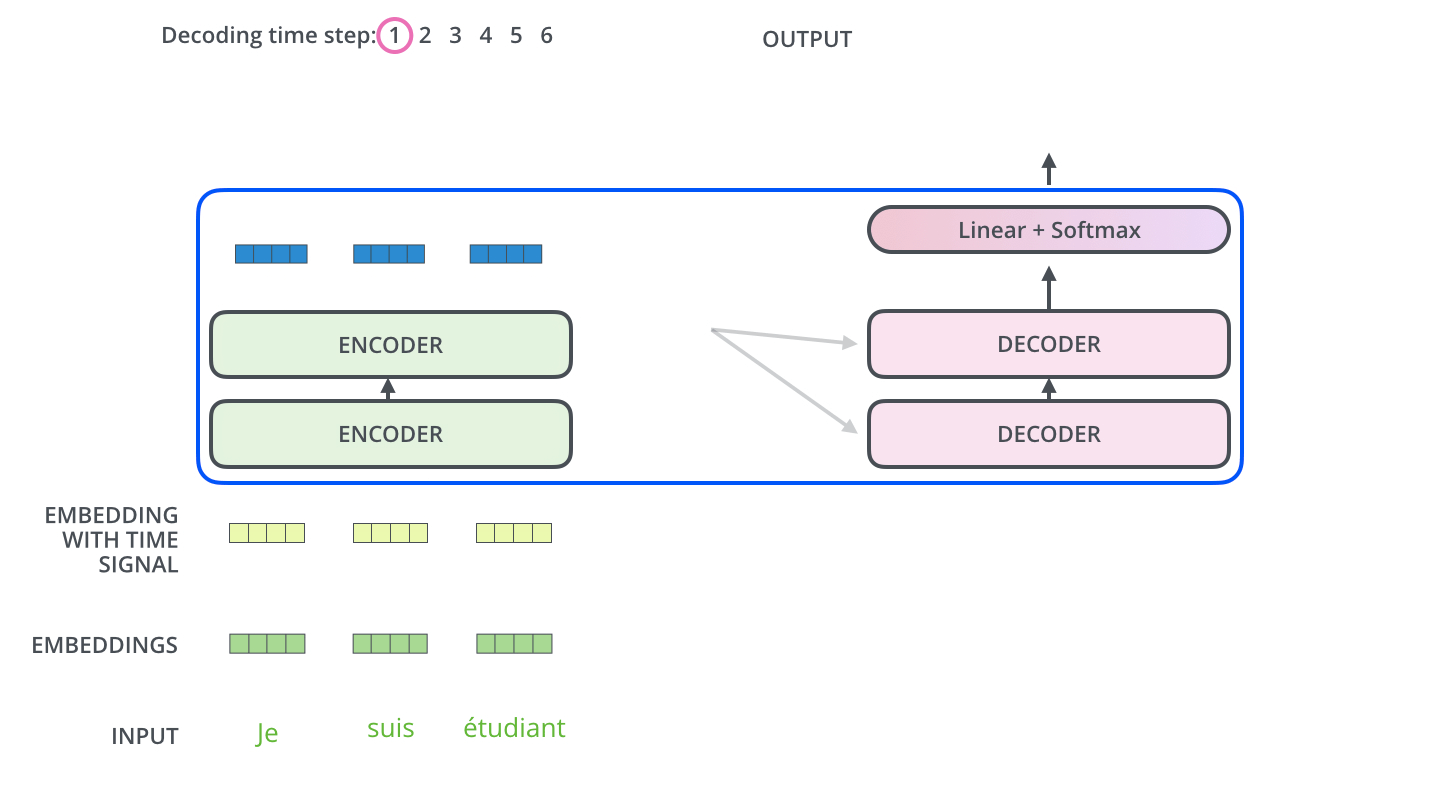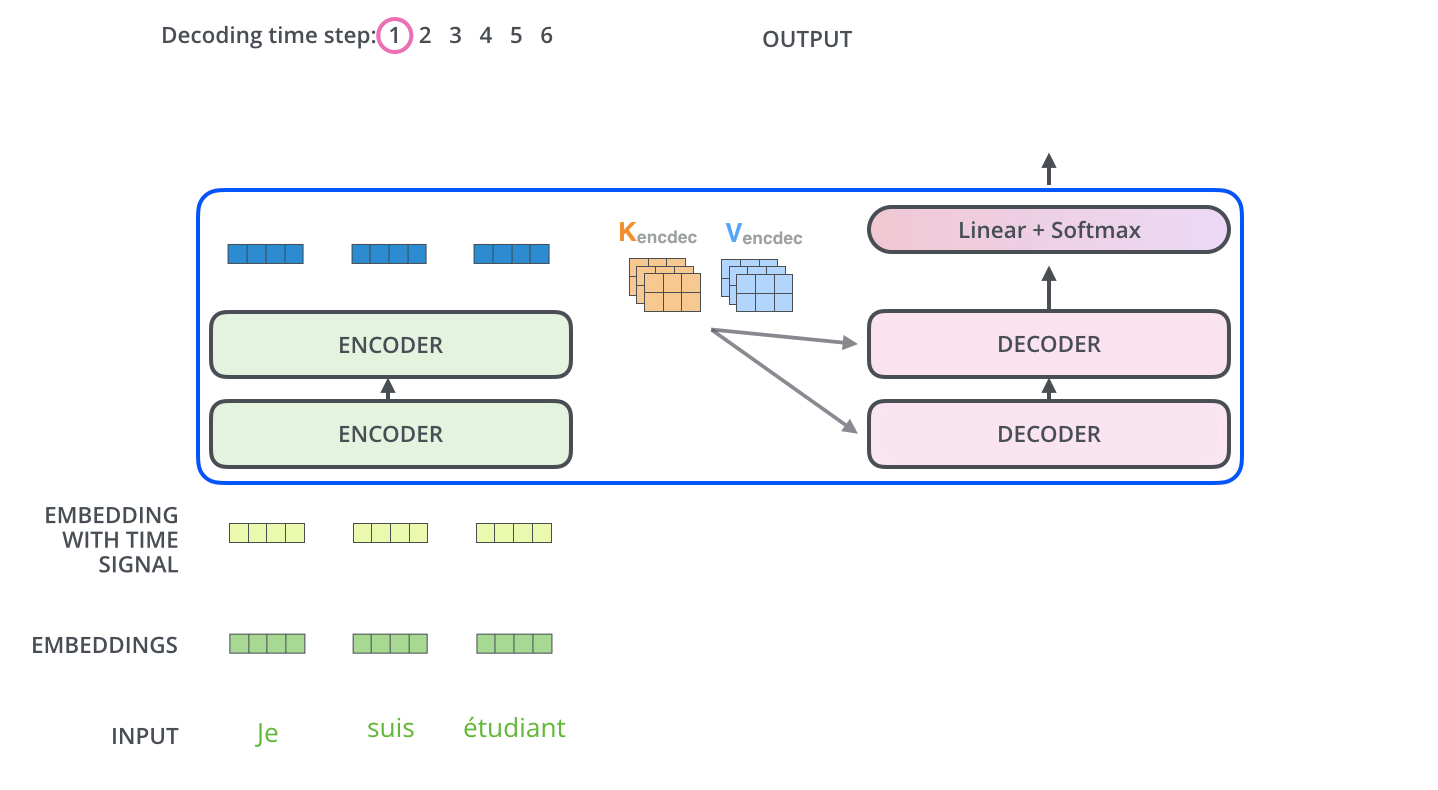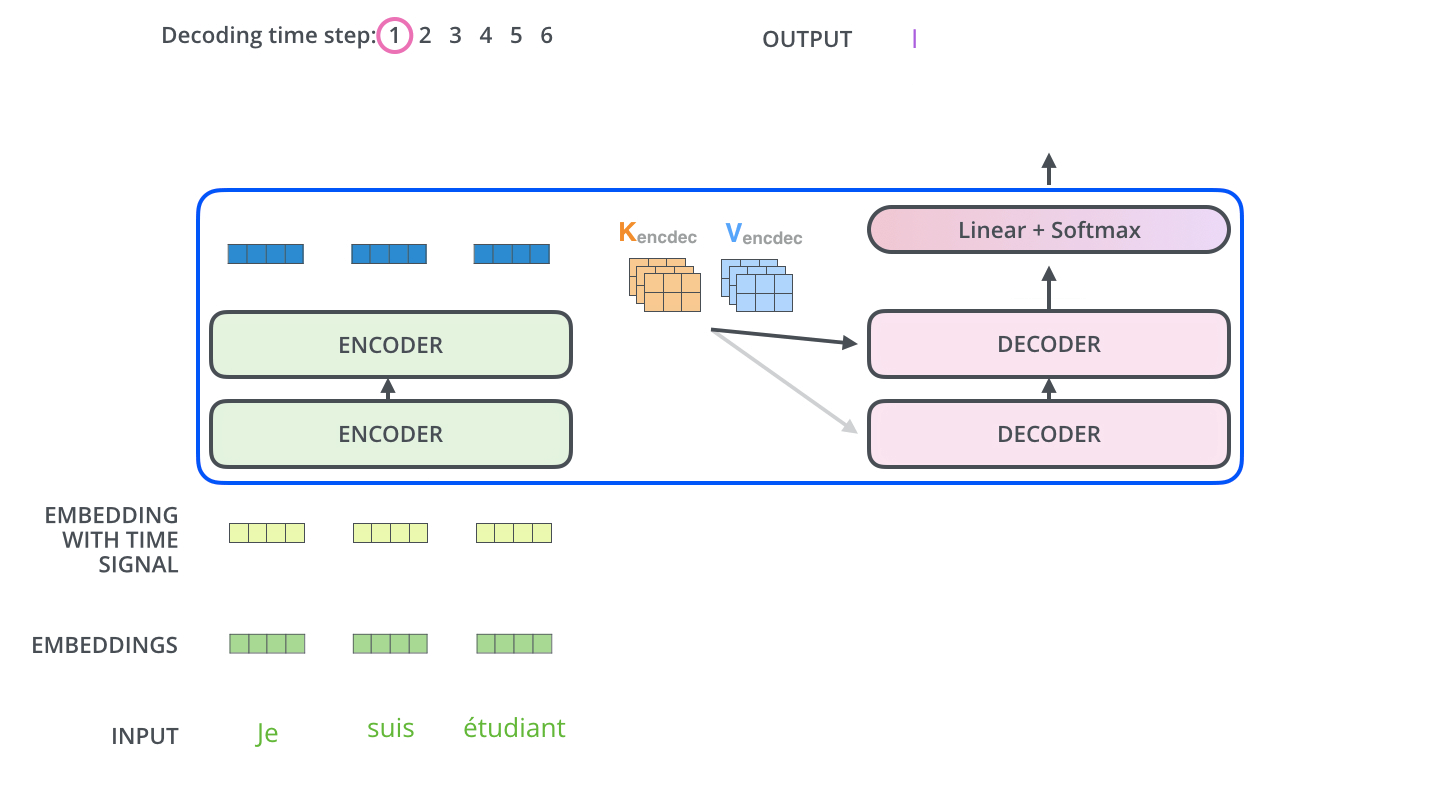
그리고 이렇게 전달된 K와 V matrix는 각각의 Decoder 내의 Encoder-Decoder Attention 모듈에서 사용됩니다. 이 K와 V는 decoder가 input sequence에서 어떤 부분에 집중해야 할 지를 알려줍니다.

Decoder

자, 이제 Encoder에서 어떻게 sequential data를 처리하고, Decoder에게 어떤 정보를 어떻게 전달해주는 지까지 봤습니다. 정말 다 왔습니다!

여기서는 이제 마지막으로 Decoder 부에서 어떤 과정을 통해 Transformer의 output을 만들어내는 지 살펴볼 것입니다.

각 step의 output은 decoder의 다음 step의 output을 만들기 위해 사용된다

Decoder 부는 전달받은 K, V와 자체적으로 생성한 Q를 이용하여 한 step마다 하나의 output을 만들어냅니다. 이렇게 만들어진 이전 step까지의 output들은 다음 step의 output을 만들기 위한 정보로 사용됩니다. (여기서 이전 step까지의 정보들도 마찬가지로 embedding과 positional encoding이 적용됩니다)

그리고 이는 다른 말로 하면, 현재 step 후의 정보들은 현재 step의 output에 영향을 주지 않는다는 것을 말합니다. 이는 모든 정보를 함께 사용하는 Encoder 부와 다른 점입니다.

현재 step 후의 정보들을 사용하지 않기 위해 decoder의 self-attention 모듈에서는 미래의 정보들을 masking(setting them to ‘-inf’)합니다. 그래서 decoder의 첫번째 self-attention 모듈은 masked-attention 모듈이라고 불립니다.

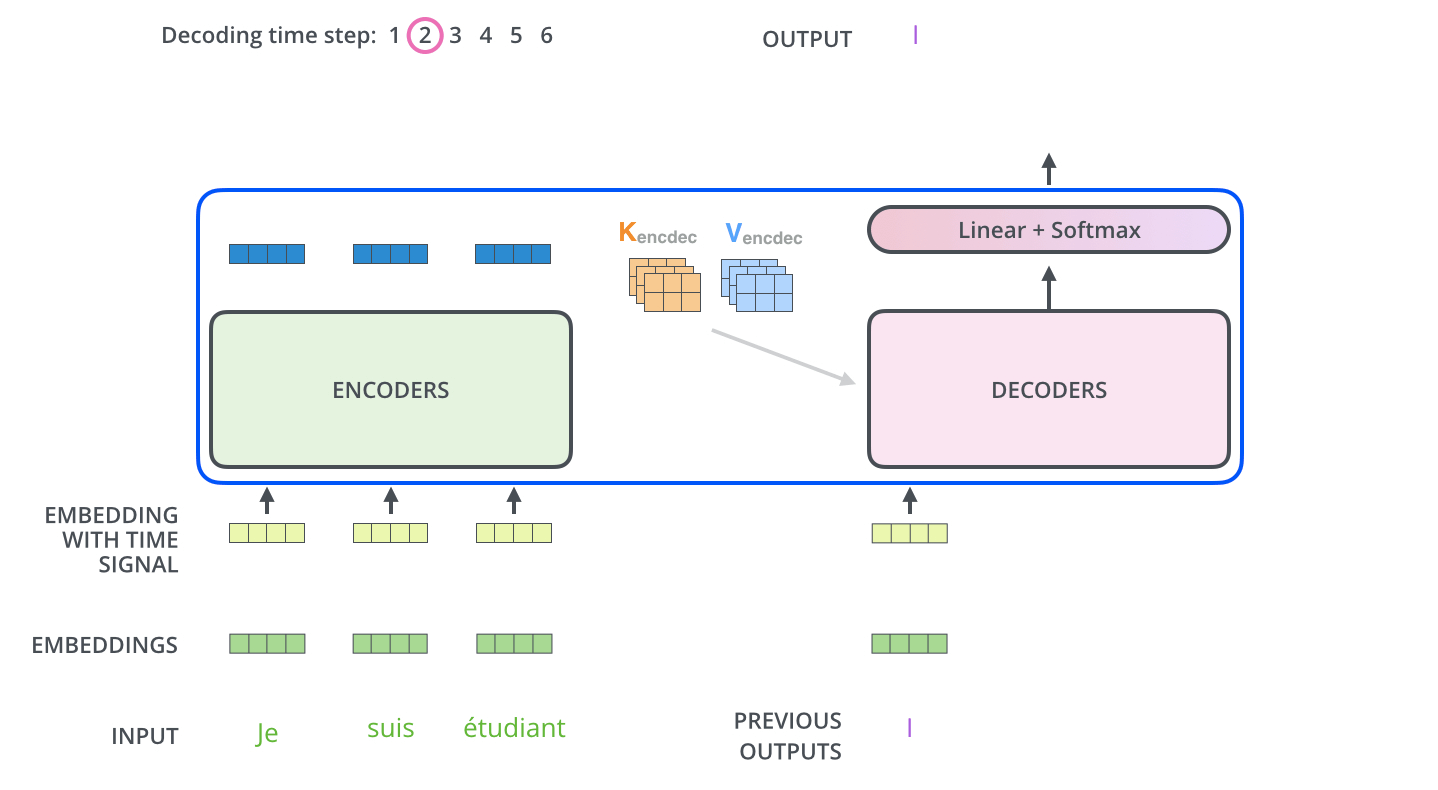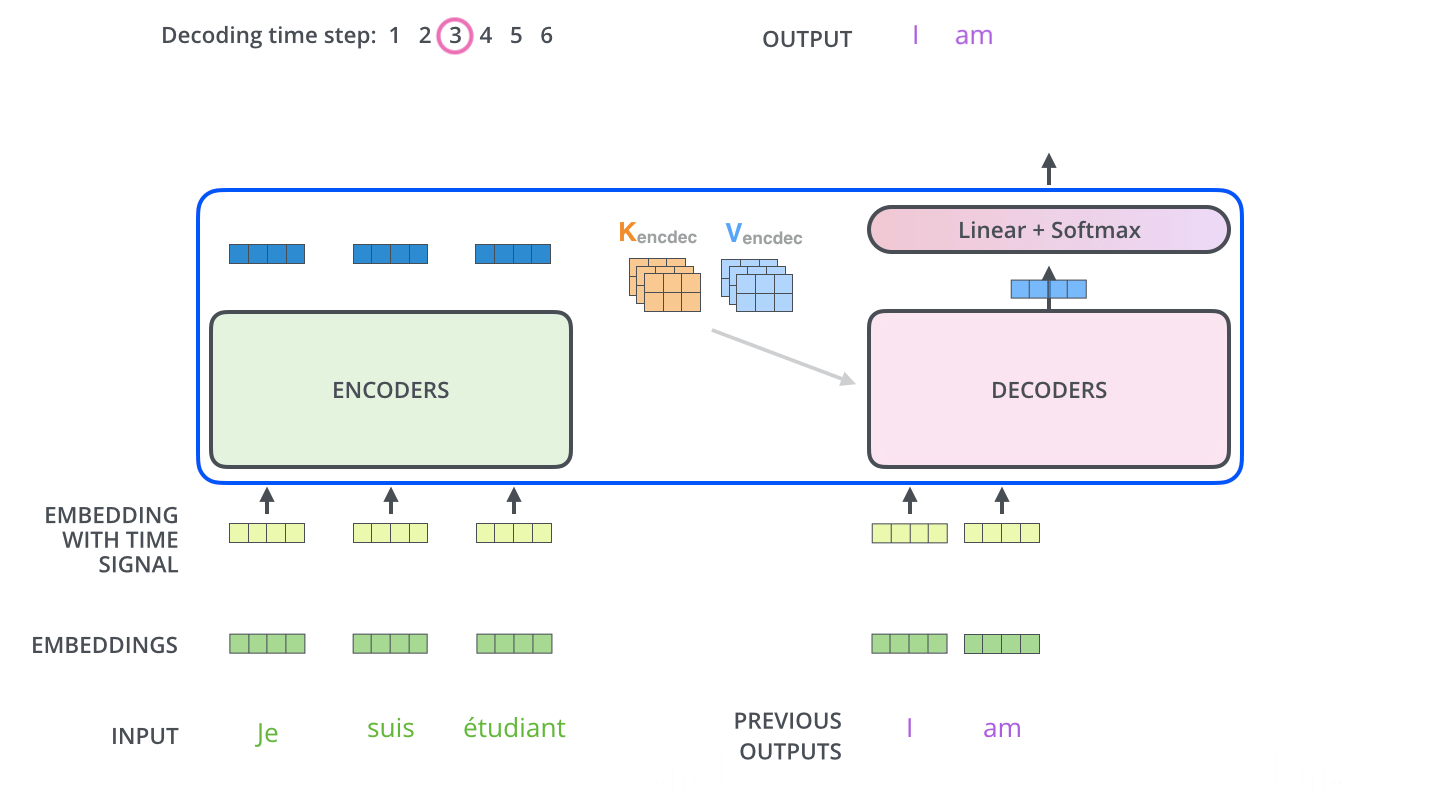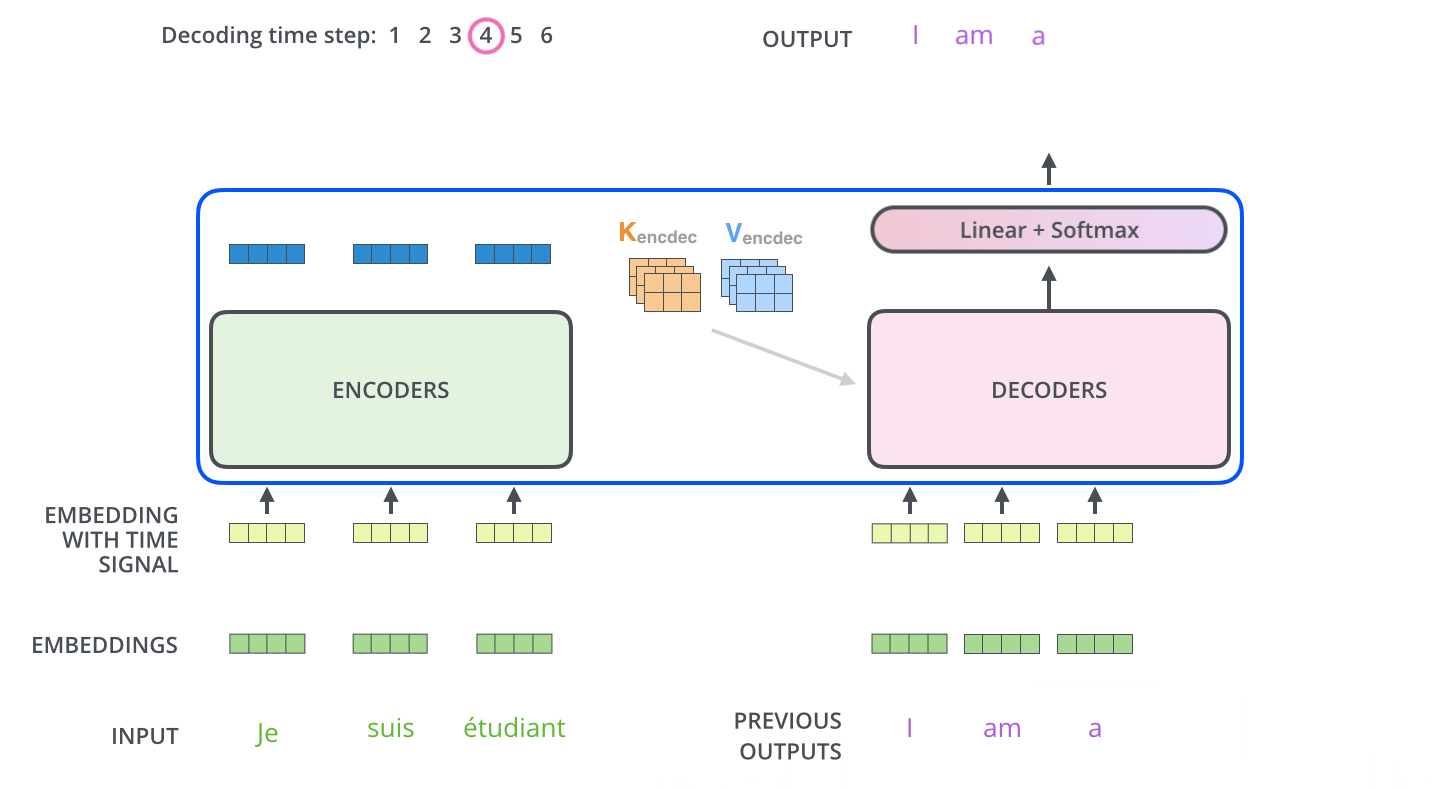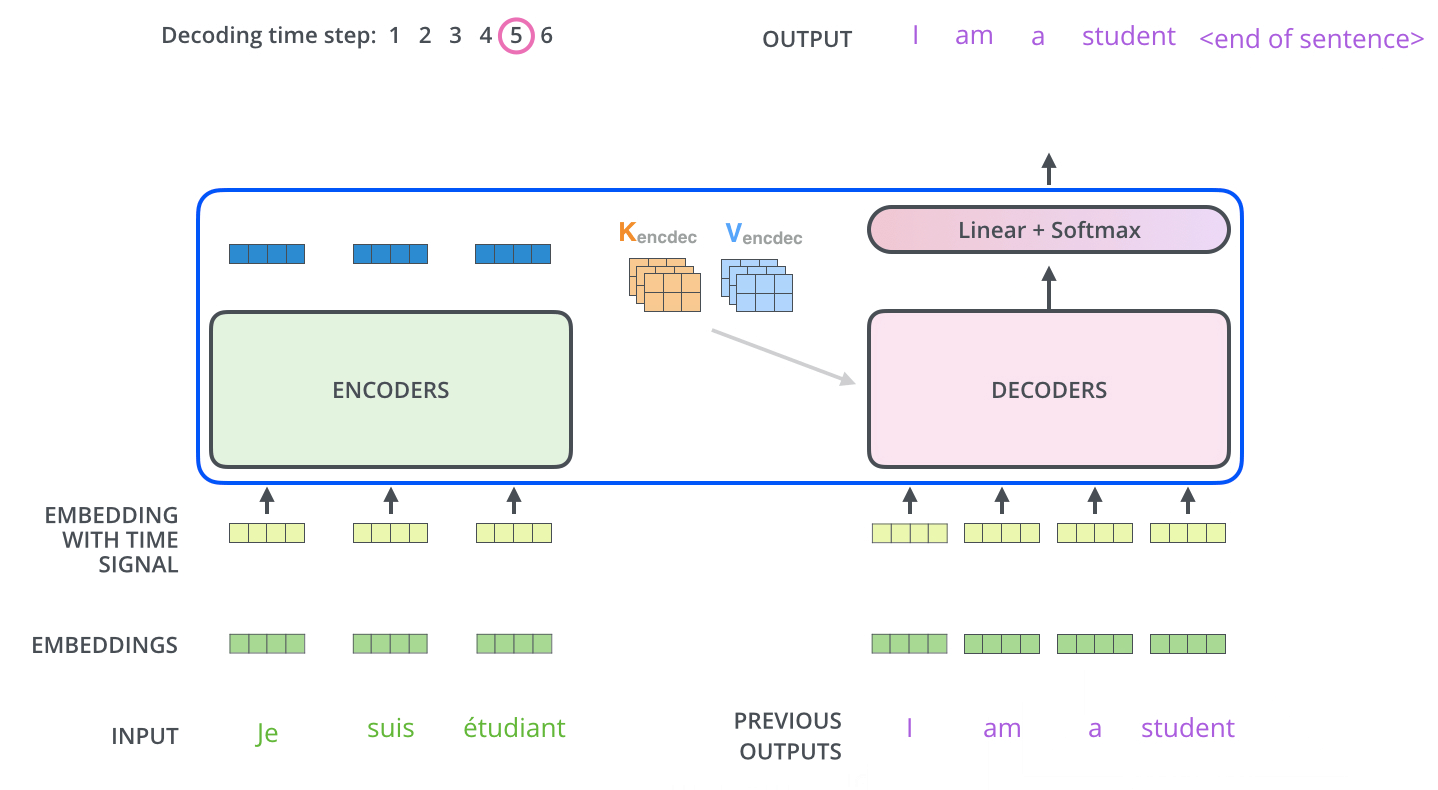
Decoder의 Encoder-Decoder Attention 모듈은 MHA(Multi-headed attention)와 동일하게 동작하며, 다른 점은 사용하는 K, V는 Encoder로부터 전달받은 값을 사용하고 Q 또한 직접 생성해내는 것이 아니라 아래 layer에서 생성된 값을 사용한다는 점입니다.

최종 Transformer 출력 생성

일련의 stacked decoder들을 지나 Decoder부의 최종 출력은 vector of floats 입니다. 이것을 어떻게 단어들로 변환할 수 있을까요?

그것이 바로 최종적으로 사용되는 Linear layer & Softmax layer의 역할입니다.

Linear Layer는 Decoder 부의 최종 output vector에 fully connect 연산을 적용하여 logits vector라는 것을 생성합니다. 그리고 이 때의 logits vector의 크기는 Transformer 모델이 알고 있는 단어의 수(output이 될 수 있는 단어 후보의 수)와 같습니다.

그리고 이 logits vector를 Softmax Layer를 거쳐 각각의 값을 확률 값으로 바꾸고, 가장 확률이 높은 값에 해당하는 단어를 이번 step의 output으로 선택하는 것이죠.

Label Smoothing

이제 Transformer의 동작 방식에 대해 모두 살펴봤습니다. 여기까지 오신 분들 축하드립니다 👏👏

근데 우리 하나만 더 보고 갑시다. 바로 Label Smoothing이라는 기술인데요, Transformer는 최종 단계에 label smoothing이라는 것을 사용해 모델의 일반화 성능을 한층 더 증가시킵니다.

이 Label smoothing에는 여러 기법들이 있는데요, Transformer에서는 Softmax layer의 출력으로 나온 probability vector를 가장 높은 확률은 가진 인덱스의 값만 1로 만드는 원-핫 방식을 사용하는 것이 아니라, 각각의 확률 값을 직접 이용하는 식으로 이를 사용합니다.

이게 무슨 말이냐 하면, 예를 들어 ‘Thank you’라는 단어를 한국어로 번역한다고 해봅시다. 이 단어는 한국어로 ‘고맙습니다’ 또는 ‘감사합니다’ 모두로 번역될 수 있습니다. 그런데 정답에 해당하는 ‘고맙습니다’에 해당하는 값만 1이라면, 모델이 그 값을 ‘감사합니다’로 예측하든 ‘짜증납니다’로 예측하든 모두 그냥 틀린 것이 되버린다는 것입니다.

이 때문에 원-핫 방식을 사용하지 않고 대신에 label smoothing을 적용하여 각각의 확률값에 유사하게 예측을 하도록 유도함으로써 모델의 일반화 성능을 한층 더 높일 수 있습니다. 이러한 label smoothing 기법은 데이터가 noisy한 경우, 즉 같은 입력 값에 다른 출력 값이 나오는 데이터들이 많을수록 크게 도움이 된다고 합니다. 자세한 내용은 더 찾아보시면 좋을 것 같습니다.

이제 정말 끝입니다! Transformer를 이해하는 것은 쉽지 않은 과정이지만, 워낙 많이 사용되고 떠오르고 있는 기술이기 때문에 이해해두면 아주 도움이 될 것이라고 생각합니다 🤗🤗

Transformer 활용의 예로는 Encoder 부분만 사용해서 이미지를 분류해내는 Visual Transformer(ViT), 텍스트의 내용에 해당하는 이미지를 생성해내는 DALL-E 등이 있습니다.

아래는 Attention 연산(Scaled Dot Product Attention, SDPA)과 MHA(Multi-Head Attention)를 구현한 코드이니, 천천히 읽어보시면서 Transformer의 과정과 그 과정이 코드로는 실제로 어떻게 구현되는지, 그 과정에서 tensor의 size에 대해 음미해보시기 바랍니다.

MHA 실습

• SDPA

  class ScaledDotProductAttention(nn.Module):
      def forward(self, Q, K, V, mask=None):
          d_K = K.size()[-1] # key dimension
          scores = Q.matmul(K.transpose(-2,-1)) / np.sqrt(d_K)
          if mask is not None:
              scores = scores.masked_fill(mask==0, -1e9) # 현재 step 후의 값 masking
          attention = F.softmax(scores, dim=-1) # Softmax
          out = attention.matmul(V) # weighted sum
          return out, attention
    
  # ==============================================================================
  # Demo run of scaled dot product attention 
  SPDA = ScaledDotProductAttention()
  n_batch,d_K,d_V = 3,128,256 # d_K(=d_Q) does not necessarily be equal to d_V
  '''
  n_Q,n_K,n_V = 30,50,50
  - Q vector의 개수와 K, V vector의 개수는 달라도 됨
  - K vector의 개수와 V vector의 개수는 같아야 함
      - Q * K.T: [n_Q, d_K]x[d_K, n_K] = [n_Q, n_K]
      - Softmax(Q*K.T/root(d_K)) * V: [n_Q, n_K]x[n_V, d_V](n_K==n_V) = [n_Q, d_V]
  '''
  n_Q,n_K,n_V = 30,50,50
  Q = torch.rand(n_batch,n_Q,d_K)
  K = torch.rand(n_batch,n_K,d_K)
  V = torch.rand(n_batch,n_V,d_V)
  out,attention = SPDA.forward(Q,K,V,mask=None)
  def sh(x): 
    return str(x.shape)[11:-1] 
  print ("SDPA: Q%s K%s V%s => out%s attention%s"%
         (sh(Q),sh(K),sh(V),sh(out),sh(attention)))
  # SDPA: Q[3, 30, 128] K[3, 50, 128] V[3, 50, 256] => out[3, 30, 256] attention[3, 30, 50]
  # ==============================================================================
  # It supports 'multi-head' attention
  n_batch,n_head,d_K,d_V = 3,5,128,256
  n_Q,n_K,n_V = 30,50,50 # n_K and n_V should be the same
  Q = torch.rand(n_batch,n_head,n_Q,d_K)
  K = torch.rand(n_batch,n_head,n_K,d_K)
  V = torch.rand(n_batch,n_head,n_V,d_V)
  out,attention = SPDA.forward(Q,K,V,mask=None)
  # out: [n_batch x n_head x n_Q x d_V]
  # attention: [n_batch x n_head x n_Q x n_K] 
  def sh(x): 
    return str(x.shape)[11:-1] 
  print ("(Multi-Head) SDPA: Q%s K%s V%s => out%s attention%s"%
         (sh(Q),sh(K),sh(V),sh(out),sh(attention)))
  # (Multi-Head) SDPA: Q[3, 5, 30, 128] K[3, 5, 50, 128] V[3, 5, 50, 256] => out[3, 5, 30, 256] attention[3, 5, 30, 50]
  

• MHA

  • Transformer 논문에서는 Attention에서 Dropout과 관련된 이야기가 없습니다만, 실제로 구현 시에는 Dropout을 사용합니다.
  • 단어의 feature의 차원수 d_feat는 n_head개의 Head에게 d_head 개씩 나눠져서 병렬적으로 처리됩니다. (d_head * n_head == d_feat)
  • Input 의 형상과 output의 형상은 일치합니다.

  class MultiHeadAttention(nn.Module):
      def __init__(self, d_feat=128, n_head=5, actv=F.relu, USE_BIAS=True, dropout_p=0.1, device=None):
          """
          : param d_feat: feature dimension(단어의 특징 차원수)
          : param n_head: number of heads(Attention 개수)
          : param actv: activation after each linear layer
          : param USE_BIAS: whether to use bias(linear layer에서 편향 사용 여부)
          : param dropout_p: dropout rate(논문에서는 드롭아웃과 관련한 설명이 없는데 구현에서는 사용)
          : device: which device to use (e.g. cuda:0)
          """
          super(MultiHeadAttention, self).__init__()
          # 단어의 특징 차원수는 attention head의 개수의 배수여야 한다. 만약 단어의 특징 차원수가 100이면 이것을
          # 하나의 attention에 한번에 넣는 것이 아니라, n_head 개의 attention에 병렬적으로 처리하기 때문이다.
          if (d_feat%n_head) != 0:
              raise ValueError("d_feat(%d) should be divisible by n_head(%d)"%(d_feat, n_head))
          self.d_feat = d_feat
          self.n_head = n_head
          self.d_head = self.d_feat // self.n_head
          self.actv = actv
          self.USE_BIAS = USE_BIAS
          self.dropout_p = dropout_p
    
          self.lin_Q = nn.Linear(self.d_feat,self.d_feat,self.USE_BIAS)
          self.lin_K = nn.Linear(self.d_feat,self.d_feat,self.USE_BIAS)
          self.lin_V = nn.Linear(self.d_feat,self.d_feat,self.USE_BIAS)
          self.lin_O = nn.Linear(self.d_feat,self.d_feat,self.USE_BIAS)
    
          self.dropout = nn.Dropout(p=self.dropout_p)
    
      def forward(self, Q, K, V, mask=None):
        """
        : param Q: [n_batch, n_Q, d_feat]
        : param K: [n_batch, n_K, d_feat]
        : param V: [n_batch, n_V, d_feat]
        : param mask
        """
        ### 필요한 feature 개수 계산
        n_batch = Q.shape[0]
        Q_feat = self.lin_Q(Q) # [n_batch, n_Q, d_feat]
        K_feat = self.lin_K(K) # [n_batch, n_K, d_feat]
        V_feat = self.lin_V(V) # [n_batch, n_V, d_feat]
    
        ### Multi-head split of Q, K, and V (d_feat = n_head*d_head)
        # [n_Q, d_head] 크기의 가중치 행렬을 n_head 개만큼 n_batch 배치수만큼 만든다. 
        Q_split = Q_feat.view(n_batch, -1, self.n_head, self.d_head).permute(0, 2, 1, 3) 
        K_split = K_feat.view(n_batch, -1, self.n_head, self.d_head).permute(0, 2, 1, 3)
        V_split = V_feat.view(n_batch, -1, self.n_head, self.d_head).permute(0, 2, 1, 3)
        # Q_split: [n_batch, n_head, n_Q, d_head]
        # K_split: [n_batch, n_head, n_K, d_head]
        # V_split: [n_batch, n_head, n_V, d_head]
    
        ### Multi-Headed Attention
        d_K = K.size()[-1] # key dimension
        scores = torch.matmul(Q_split, K_split.permute(0,1,3,2)) / np.sqrt(d_K) # [n_batch, n_head, n_Q, n_K]
        if mask is not None:
            scores = scores.masked_fill(mask==0, -1e9)
        attention = torch.softmax(scores, dim=-1)
        # dropout is NOT mentioned in the paper!
        x_raw = torch.matmul(self.dropout(attention), V_split) # [n_batch, n_head, n_Q, d_head] (n_K==n_V)
    
        ### Reshape x
        x_rsh1 = x_raw.permute(0,2,1,3).contiguous()   # [n_batch, n_Q, n_head, d_head]
        x_rsh2 = x_rsh1.view(n_batch, -1, self.d_feat) # [n_batch, n_Q, d_feat]
    
        ### Linear
        x = self.lin_O(x_rsh2) # [n_batch, n_Q, d_feat]
        out = {'Q_feat':Q_feat,'K_feat':K_feat,'V_feat':V_feat,
               'Q_split':Q_split,'K_split':K_split,'V_split':V_split,
               'scores':scores,'attention':attention,
               'x_raw':x_raw,'x_rsh1':x_rsh1,'x_rsh2':x_rsh2,'x':x}
        return out
    
    
  # ==============================================================================
  # Self-Attention Layer
  n_batch = 128
  n_src   = 32
  d_feat  = 200
  n_head  = 5
  src = torch.rand(n_batch,n_src,d_feat)
  self_attention = MultiHeadAttention(
      d_feat=d_feat,n_head=n_head,actv=F.relu,USE_BIAS=True,dropout_p=0.1,device=device)
  out = self_attention.forward(src,src,src,mask=None)
    
  Q_feat,K_feat,V_feat = out['Q_feat'],out['K_feat'],out['V_feat']
  Q_split,K_split,V_split = out['Q_split'],out['K_split'],out['V_split']
  scores,attention = out['scores'],out['attention']
  x_raw,x_rsh1,x_rsh2,x = out['x_raw'],out['x_rsh1'],out['x_rsh2'],out['x']
    
  # Print out shapes
  def sh(_x): 
    return str(_x.shape)[11:-1] 
  print ("Input src:\t%s  \t= [n_batch, n_src, d_feat]"%(sh(src)))
  print ()
  print ("Q_feat:   \t%s  \t= [n_batch, n_src, d_feat]"%(sh(Q_feat)))
  print ("K_feat:   \t%s  \t= [n_batch, n_src, d_feat]"%(sh(K_feat)))
  print ("V_feat:   \t%s  \t= [n_batch, n_src, d_feat]"%(sh(V_feat)))
  print ()
  print ("Q_split:  \t%s  \t= [n_batch, n_head, n_src, d_head](d_head * n_head == d_feat)"%(sh(Q_split)))
  print ("K_split:  \t%s  \t= [n_batch, n_head, n_src, d_head](d_head * n_head == d_feat)"%(sh(K_split)))
  print ("V_split:  \t%s  \t= [n_batch, n_head, n_src, d_head](d_head * n_head == d_feat)"%(sh(V_split)))
  print ()
  print ("scores:   \t%s  \t= [n_batch, n_head, n_src, n_src](Q_split * K_split)"%(sh(scores)))
  print ("attention:\t%s  \t= [n_batch, n_head, n_src, n_src]"%(sh(attention)))
  print ()
  print ("x_raw:    \t%s  \t= [n_batch, n_head, n_src, d_head](x_raw=Attention(src,Q,K,V))"%(sh(x_raw)))
  print ("x_rsh1:   \t%s  \t= [n_batch, n_src, n_head, d_head]"%(sh(x_rsh1)))
  print ("x_rsh2:   \t%s  \t= [n_batch, n_src, d_feat]"%(sh(x_rsh2)))
  print ()
  print ("Output x: \t%s  \t= [n_batch, n_src, d_feat](output shape == input shape)"%(sh(x)))
    
  '''
  Input src:	[128, 32, 200]  	= [n_batch, n_src, d_feat]
    
  Q_feat:   	[128, 32, 200]  	= [n_batch, n_src, d_feat]
  K_feat:   	[128, 32, 200]  	= [n_batch, n_src, d_feat]
  V_feat:   	[128, 32, 200]  	= [n_batch, n_src, d_feat]
    
  Q_split:  	[128, 5, 32, 40]  	= [n_batch, n_head, n_src, d_head](d_head * n_head == d_feat)
  K_split:  	[128, 5, 32, 40]  	= [n_batch, n_head, n_src, d_head](d_head * n_head == d_feat)
  V_split:  	[128, 5, 32, 40]  	= [n_batch, n_head, n_src, d_head](d_head * n_head == d_feat)
    
  scores:   	[128, 5, 32, 32]  	= [n_batch, n_head, n_src, n_src](Q_split * K_split)
  attention:	[128, 5, 32, 32]  	= [n_batch, n_head, n_src, n_src]
    
  x_raw:    	[128, 5, 32, 40]  	= [n_batch, n_head, n_src, d_head](x_raw=Attention(src,Q,K,V))
  x_rsh1:   	[128, 32, 5, 40]  	= [n_batch, n_src, n_head, d_head]
  x_rsh2:   	[128, 32, 200]  	= [n_batch, n_src, d_feat]
    
  Output x: 	[128, 32, 200]  	= [n_batch, n_src, d_feat](output shape == input shape)
  '''
  

참고 자료

• Attention Is All You Need 논문
• Transformer 설명 블로그(영어)
• Transformer 논문 리뷰 유튜브 영상(한글)